Cubic problems.
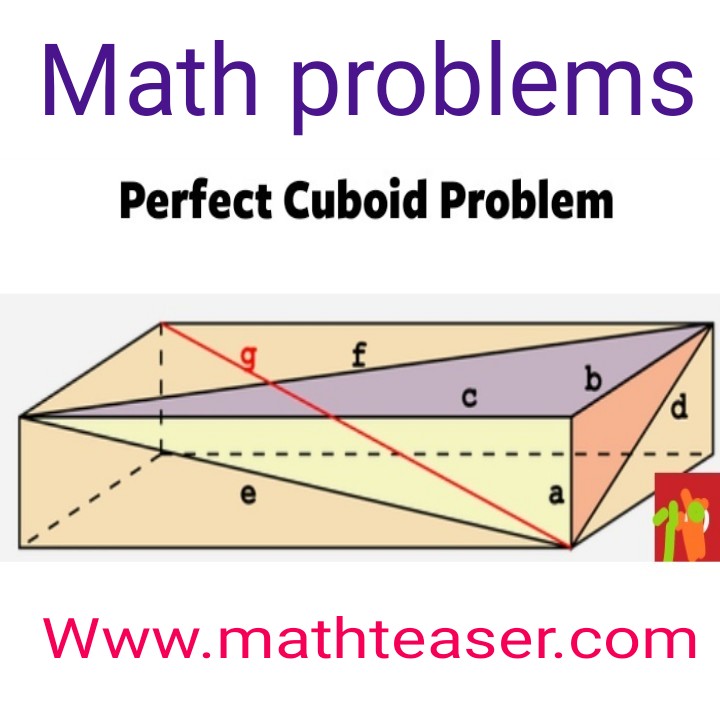
Remember the pythagorean theorem, A2 + B2 = C2? The three letters correspond to the three sides of a right triangle. In a Pythagorean triangle, and all three sides are whole numbers. Let’s extend this idea to three dimensions. In three dimensions, there are four numbers. In the image above, they are A, B, C, and G. The first three are the dimensions of a box, and G is the diagonal running from one of the top corners to the opposite bottom corner.
Just as there are some triangles where all three sides are whole numbers, there are also some boxes where the three sides and the spatial diagonal (A, B, C, and G) are whole numbers. But there are also three more diagonals on the three surfaces (D, E, and F) and that raises an interesting question: can there be a box where all seven of these lengths are integers?
The goal is to find a box where A2 + B2 + C2 = G2, and where all seven numbers are integers. This is called a perfect cuboid. Mathematicians have tried many different possibilities and have yet to find a single one that works. But they also haven’t been able to prove that such a box doesn’t exist, so the hunt is on for a perfect cuboid.