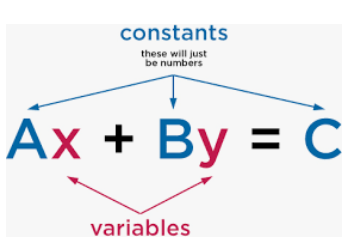
Algebra problems questions

Students are always confusing to understand algebra so many people said it algebra problems in the starting to understanding the algebra too difficult after solving it become very easy so don’t worry in algebra problems
Find the sum to infinity of the series 12 + 22. x + 32.x2 + 42.x3 +…,…. |x| < 1.
Solution: Though the given series is not an Arithmetico-Geometric series, however, the differences (22 – 12), (32 – 22) , …..form an AP. So, we can use the Method of Differences.
Let S = 1 + 4x + 9x2 +16x3 +…. ∞.
Multiply both sides with common ratio x of the GP.
Sx = x + 4x2 + 9x3 +……∞.
Now, subtract the two equations.
=> (1 – x) S = 1 + 3x + 5x2 + 7x3 +….∞ ……. (1)
Now, let R = 1 + 3x + 5x2 + 7x3 +…∞, which is an Arithmetico-Geometric series with a = 1, d = 2 and r = x.
For an A.G.P,
Sum R = 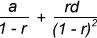 ,
,
Substituting the values, we get R = 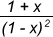 ,
,
Substitute R in (1), we get,
(1 – x) S = 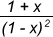
⇒ S = 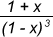 ,
,